In a previous post I showed how it is possible to write asynchronous code in a direct style using the ContT monad. Here, I’ll extend the idea further and present an implementation of a very simple FRP library based on continuations.

{-# LANGUAGE DoRec, BangPatterns #-}
import Control.Applicative
import Control.Monad
import Control.Monad.IO.Class
import Data.IORef
import Data.Monoid
import Data.Void

Monadic events

Let’s start by defining a callback-based Event type:

newtype Event a = Event { on :: (a -> IO ()) -> IO Dispose }

A value of type Event a represents a stream of values of type a, each occurring some time in the future. The on function connects a callback to an event, and returns an object of type Dispose, which can be used to disconnect from the event:

newtype Dispose = Dispose { dispose :: IO () }

instance Monoid Dispose where
  mempty = Dispose (return ())
  mappend d1 d2 = Dispose $ do
    dispose d1
    dispose d2

The interesting thing about this Event type is that, like the simpler variant we defined in the above post, it forms a monad:

instance Monad Event where

First of all, given a value of type a, we can create an event occurring “now” and never again:

  return x = Event $ \k -> k x >> return mempty

Note that the notion of “time” for an Event is relative.

All time-dependent notions about Events are formulated in terms of a particular “zero” time, but this origin of times is not explicitly specified.

This makes sense, because, even though the definition of Event uses the IO monad, an Event object, in itself, is an immutable value, and can be reused multiple times, possibly with different starting times.

  e >>= f = Event $ \k -> do
    dref <- newIORef mempty
    addD dref e $ \x ->
      addD dref (f x) k
    return . Dispose $
      readIORef dref >>= dispose

addD :: IORef Dispose -> Event a -> (a -> IO ()) -> IO ()
addD d e act = do
  d' <- on e act
  modifyIORef d (`mappend` d')

The definition of >>= is slightly more involved.

We call the function f every time an event occurs, and we connect to the resulting event each time using the helper function addD, accumulating the corresponding Dispose object in an IORef.

The resulting Dispose object is a function that reads the IORef accumulator and calls dispose on that.

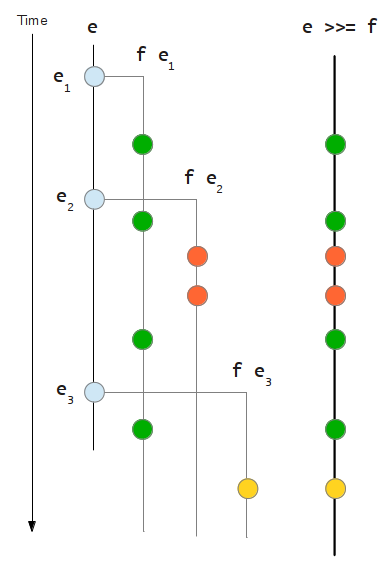
As the diagram shows, the resulting event e >>= f includes occurrences of all the events originating from the occurrences of the initial event e.

Event union

Classic FRP comes with a number of combinators to manipulate event streams. One of the most important is event union, which consists in merging two or more event streams into a single one.

In our case, event union can be implemented very easily as an Alternative instance:

instance Functor Event where
  fmap = liftM

instance Applicative Event where
  pure = return
  (<*>) = ap

instance Alternative Event where
  empty = Event $ \_ -> return mempty
  e1 <|> e2 = Event $ \k -> do
    d1 <- on e1 k
    d2 <- on e2 k
    return $ d1 <> d2

An empty Event never invokes its callback, and the union of two events is implemented by connecting a callback to both events simultaneously.

Other combinators

We need an extra primitive combinator in terms of which all other FRP combinators can be implemented using the Monad and Alternative instances.

once :: Event a -> Event a
once e = Event $ \k -> do
  rec d <- on e $ \x -> do
             dispose d
             k x
  return d

The once combinator truncates an event stream at its first occurrence. It can be used to implement a number of different combinators by recursion.

accumE :: a -> Event (a -> a) -> Event a
accumE x e = do
  f <- once e
  let !x' = f x
  pure x' <|> accumE x' e

takeE :: Int -> Event a -> Event a
takeE 0 _ = empty
takeE 1 e = once e
takeE n e | n > 1 = do
  x <- once e
  pure x <|> takeE (n - 1) e
takeE _ _ = error "takeE: n must be non-negative"

dropE :: Int -> Event a -> Event a
dropE n e = replicateM_ n (once e) >> e

Behaviors and side effects

We address behaviors and side effects the same way, using IO actions, and a MonadIO instance for Event:

instance MonadIO Event where
  liftIO m = Event $ \k -> do
    m >>= k
    return mempty

newtype Behavior a = Behavior { valueB :: IO a }

getB :: Behavior a -> Event a
getB = liftIO . valueB

Now we can implement something like the apply combinator in reactive-banana:

apply :: Behavior (a -> b) -> Event a -> Event b
apply b e = do
  x <- e
  f <- getB b
  return $ f x

Events can also perform arbitrary IO actions, which is necessary to actually connect an Event to user-visible effects:

log :: Show a => Event a -> Event ()
log e = e >>= liftIO . print

Executing event descriptions

An entire GUI program can be expressed as an Event value, usually by combining a number of basic events using the Alternative instance.

A complete program can be run with:

runEvent :: Event Void -> IO ()
runEvent e = void $ on e absurd

runEvent_ :: Event a -> IO ()
runEvent_ = runEvent . (>> empty)

Underlying assumptions

For this simple system to work, events need to possess certain properties that guarantee that our implementations of the basic combinators make sense.

First of all, callbacks must be invoked sequentially, in the order of occurrence of their respective events.

Furthermore, we assume that callbacks for the same event (or simultaneous events) will be called in the order of connection.

Many event-driven frameworks provide those guarantees directly. For those that do not, a driver can be written converting underlying events to Event values satisfying the required ordering properties.

Conclusion

It’s not immediately clear whether this approach can scale to real-world GUI applications.

Although the implementation presented here is quite simplistic, it could certainly be made more efficient by, for example, making Dispose stricter, or adding more information to Event to simplify some common special cases.

This continuation-based API is a lot more powerful than the usual FRP combinator set. The Event type combines the functionalities of both the classic Event and Behavior types, and it offers a wider interface (Monad rather than only Applicative).

On the other hand, it is a lot less safe, in a way, since it allows to freely mix IO actions with event descriptions, and doesn’t enforce a definite separation between the two. Libraries like reactive-banana do so by distinguishing beween “network descriptions” and events/behaviors.

Finally, there is really no sharing of intermediate events, so expensive computations occurring, say, inside an accumE can end up being unnecessarily performed more than once.

This is not just an implementation issue, but a consequence of the strict equality model that this FRP formulation employs. Even if two events are identical, they might not actually behave the same when they are used, because they are going to be “activated” at different times.